Radical and
Rational Functions
Radical Function is a function that includes a radical with a
variable in the radicand
Example: √3x
Graphing Radical Functions
For this lesson it is important to remember the concepts that
we learned during the transformations unit 2.
In the graph above transformations were done only on the y
values and the x values stay the same.
It is also important to remember that the number inside the
radicand in the cases above cannot be < 0.
Example:
y=2√x Vertical translation by a factor of 2
y= -2√x Vertical translation by a factor of 2 and reflection
on the x axis
Solving the Equation of Radical and Linear Functions
G(x) = x-5
We can solve this by using the table of values. Since there
is no radicand there is no restriction on the domain and range of the function.
F(x) = (√x-3)
There is a restriction on the domain since the value inside
the radicand cannot be less than 0.
x≥3
Another way to solve this is algebraically.
x-5 = (√x-3)
1. Square both
sides to get rid of the radicand symbol in f(x).
(x-5)2 = x-3
2. Square the
equation (x-5)2.
x2-10x+25 = x-3
3. Solve for
x.
x2-11x+28 = 0
(x-7)(x-4) = 0
(x-7) =0
or (x-4) = 0
x= 7 or x= 4
Check to see if the solutions are correct.
x-5=(√x-3) x=4
x=7 4-5=(√4-3)
7-5=(√7-3) -1=√1
2=√4 -1≠1
2=2
Thank you for a great class and semester, Mr.P!



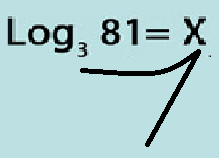



.jpeg)

















